ドンドン成績が上がっていく子
ある時期がくると、自分で勉強を始める子がいます。ドンドン成績が上がっていく子がいます。一方で、いつまでも、なかなかかわらない子もいます。
その違いは・・・
小５年夏からの１年間は、義務教育９年間の最大の上り坂です。
それを、問題を形の上から見ると、
５年前半まで : １.６cmの厚さの本を４２冊かさねたら何cmになりますか。
５年後半以降 : １６本で１２８０円のペンを９本買えば代金はいくらですか。
５年生の前半までは、問題文中に出てくる数字は２種類がほとんどです。だから、問題を読めば、足すのか、引くのか、かけるのか、わるのか、すぐにわかります。計算の１回でおしまいです。
ところが、５年生後半以降の問題では、問題文中に３種類以上の数字が出てきます。ということは、問題文に出てきた数字同士の関係を考えることからスタートします。計算を考えることは、その後になります。
考えるための道具をもっているか
しかも、そろそろ、分数が出ることが、当たり前になりましたから、数量関係を考えることが、整数の時よりつかみにくくなってきています。そこで、考えるためのツール・道具を、上手に使えるかどうかが問題になってきます。ツール・道具としては、線分図・面積図が一般的です。
Ｍａｘの対応表は何にでも使える
ここにＭａｘ流の『対応表』を加えましょう。
子どもたちは、線分図・面積図より使いやすいといいます。学校の教科書には、『対応表』は載っていません。似たものはあります。これは、完全なＭａｘオリジナルではありませんが、Max流に加工して、子どもたちには扱いやすすいツールにしています。
去年の中３生で、数学が苦手な子でしたが、中３の１２月ぐらいに、「先生、『対応表』って何にでも使えてカンタンでいいね。わかりやす」と言った子がいました。「だから、小５から教えている」と言ったら、「小5で、これが使えたら無敵ですね。戻りたい」と言っていました。
学校の教科書では、線分図・面積図で説明しています。使用する図の違いはありますが、問題はここからです。
その図を描けという問題がないのです。教科書を確認してください（さらに、本屋さんで、学習参考書を覗いてみてください）。子どもたちは、説明を受けるときは、それらの図を使って説明を受けます。
でも、「描きなさい」という練習がないので、なかなか自分で考えるために図を描けるようになっていないのです。だから、ツール・道具が使えないままになっているのです。
もう1点、子どもの意識として、「パッ」とすぐにできることが、できることと勘違いしている子もたくさんいます。
Maxは、ココに時間をかけます。
考えるための道具・ツールが使えない。このへんが、中学・高校生と学年が上がるほど、泣き所になってきます。いすれも小5の夏～小6の夏の1年間で学習します。「義務教育９年間の最大の上り坂」の由縁です。これらすべての単元で、『対応表』が使えます。
最重要中の最重要 「単位あたりの大きさ」「 百分率」「 分数と小数」「 分数のたし算とひき算」「速さ」を学習する際に、書いて説明するだけでなく、自分で問題を解く時に、まず対応表をつくって、対応表をみて、何算をするかを考えるという手順で授業を進めます。
教科書で４ページしか無いのに。
小5の「分数と小数」という単元は、教科書で４ページしかありません。しかも、ここを習っているときは、簡単に思います。しかし、後から、大きな影響を与える単元です。ほとんど致命傷になっている単元です。
何かの時にお子さんが、「割り切れない」と言ったらその悪い例の見本のような状態です。割り切れなければ、分数にする。この意識転換ができていない子が大半です。 そのまま、中学生になれば、数学で、いい思いはできませんね。
数学では、4÷6 を割り算することは稀です。
と分数にして進んでいきます。
たったこれだけのことですが、何の抵抗もなしに、自然に分数で処理で処理する子と「割り切れません」といっている子の差は、とてつもなく大きいものがあります。後から伸びていく子とそうでない子の大きな差です。
小学生～高校生までを教えているからわかる、考える力を伸ばす算数のポイント・ずっと伸びていけるポイント。
分数と整数のかけ算・わり算
考え方は、５年の時と同じです。ただし、小６では、整数だけでなく、分数や小数も出てきます。まずは、『対応表』の作り方の復習を、整数でやってみましょう。
対応表の作り方
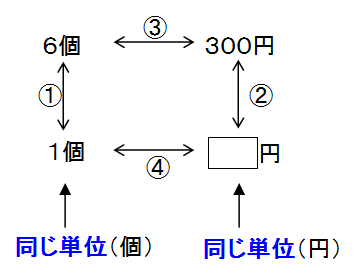
例 : 「６個で３００円の消しゴム１個の値段は何円ですか」
●同じ単位の数をたてに並べる
①,②は同じ関係。 ①は下から上に６倍（×6）だから、逆に上から下は÷６ ②も上から下は÷６になるから、 （答）300円÷6＝50円 小6で、ここに分数が登場します。分数があってもまったく同じことをするだけです。
対応表での考え方
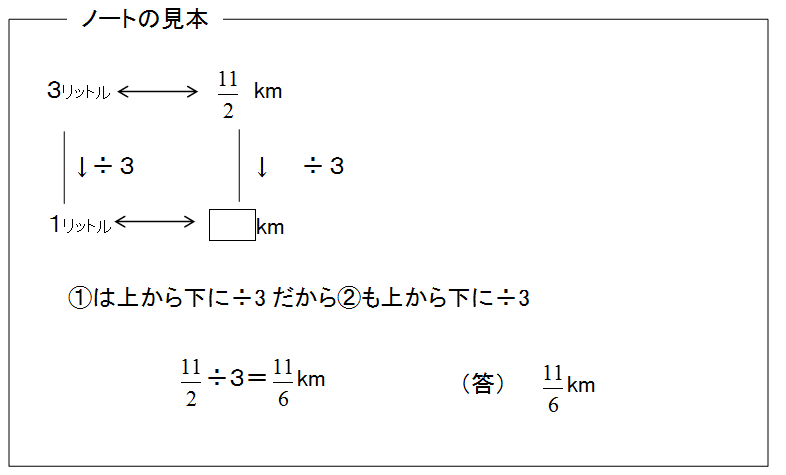
問題：「３リットルのガソリンで
km走る自動車は、１リットルのガソリンで何Km走るか」 
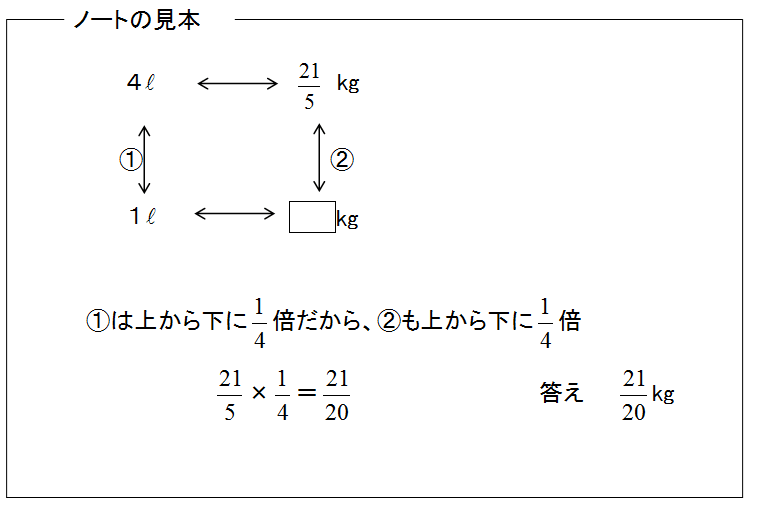
問題： 「米４L の重さをはかったら、
kgありました。この米1L の重さは何kgですか。」 
◆鶴ヶ谷教室 ☎252-0998 989-0824 宮城野区鶴ヶ谷4-3-1
◆幸 町 教室 ☎295-3303 983-0836 宮城野区幸町3-4-19
電話でのお問合せ AM10:30～PM22:30