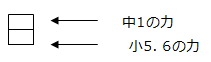「できる子のスタート」は、もう始まっています
最近、こんなことはありませんか?
- 難しい問題になると、すぐ「わからない」と言ってしまう
- 授業で“どこまで理解しているか”がよくわからない
- 昔は算数が好きだったのに、最近あまり自信がなさそう
実は今、お子さまにとって、学力の“土台”を築く最後のチャンスが来ています。
この春からの数ヶ月は、「できる子」としてのサイクルに乗るかどうかの分かれ道。
マックスでは、これまで多くの“ぐんと伸びる子”たちを見てきました。
その子たちには、ある共通点があります。
📘 学年を超えて起きた、ある授業の出来事
春の集中授業では、いろいろな学年の子が同じ時間帯に来ています。
そんなある日、教室でこんな会話がありました。
先生:「20分って、時間にすると何時間かな?」
中3Aくん:「えっと…0.2時間です!」
先生:「ん?それだと60分は0.6時間になっちゃうけど…?」
中3Aくん:「あれ、違うんですか!?」
そこで、小6のCちゃんに聞いてみました。
先生:「Cちゃん、ちょっとだけ聞いてもいい?」
Cちゃん:「えっと…20分は、3分の1時間です。」
先生:「はい、正解!」
教室にいた中3の子たちは思わず驚きの声をあげました。
「えっ、小学生なのにわかるの!? すごい!」
こうしたことは、マックスでは日常的にあります。
“中学生になれば自然にできるようになる”わけではないのです。
むしろ、小5〜小6でつくった土台の大きさが、これからの学習に大きく影響するのです。
🧱 「土台」が大きければ、大きな力が積み上がる
しっかりとした土台がある子は、中学生になっても無理なく学力を伸ばしていきます。
逆に、土台がぐらついていると、努力してもすぐ崩れてしまう。
こんなことが実際によくあります。
そして結果的に、
「やったけどダメだった」
という、子どもにとって一番つらい経験につながってしまうことも。
だからこそ、“小6の今”は、将来の伸びを大きく左右する時期なのです。
🌱「自分はできる」と思える子は、伸びる
成績の良い中学生・高校生の多くに共通するのは、「自分はできる」という感覚を持っていること。
これは、特別な才能ではありません。
「小学生のころ、先生に褒められた」
「友達から“すごいね”って言われた」
そんな小さな成功体験が、「自分はできる」という自信を育てているのです。
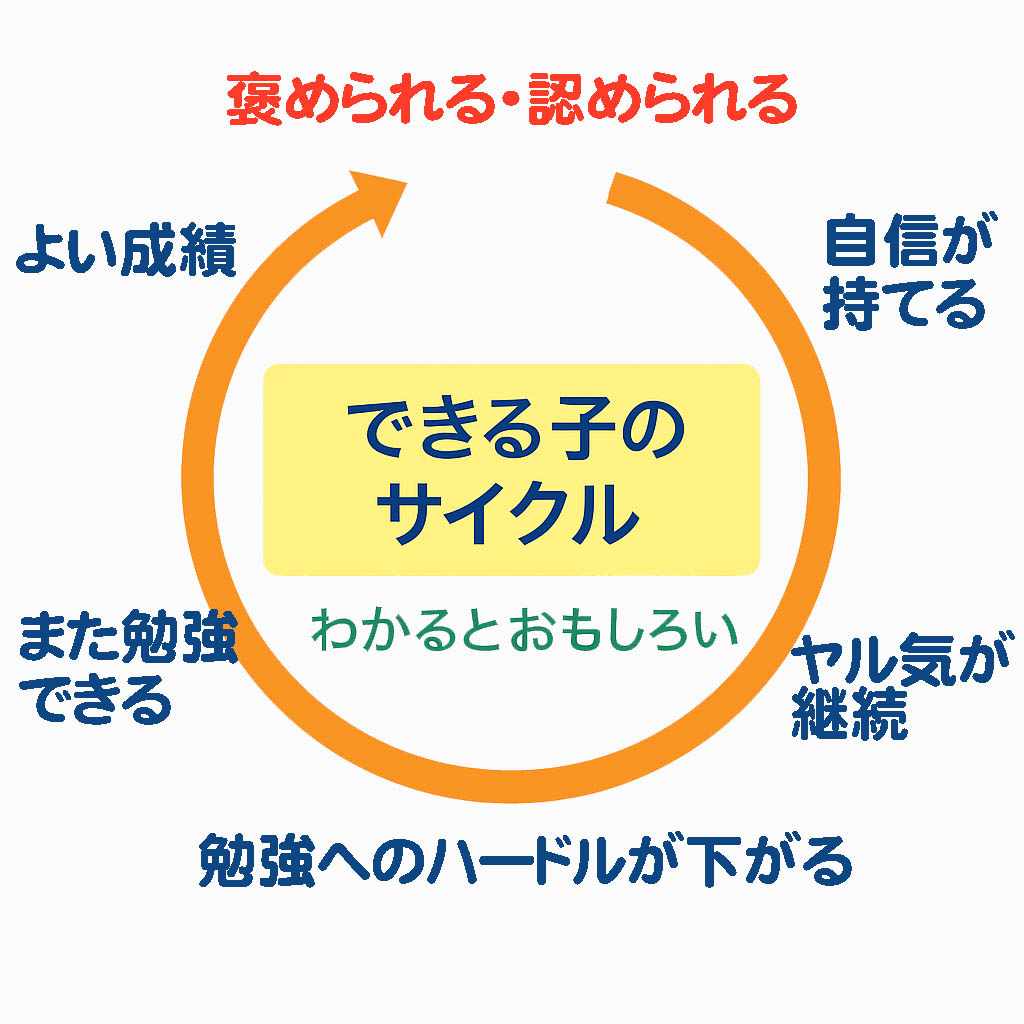
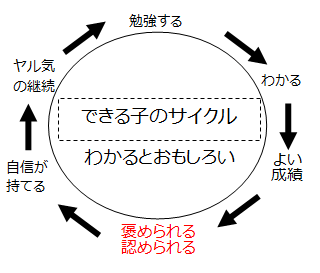
🔁 「できる子のサイクル」に乗ると、自然に伸びる

▶ 褒められる
→ 自信がつく
→ 前向きに取り組む
→ 勉強時間が増える
→ 成績が上がる
→ また褒められる
→ …(繰り返す)
このサイクルを早く回し始めた子ほど、自然に学ぶ習慣が身につき、長期的に伸びていきます。
📐 なぜ「算数」がカギになるのか?
小学生の間では、算数ができる子=頭がいい子、と思われがちです。
だからこそ――
- 算数ができる子は、自信を持ちやすく
- 算数が苦手な子は、自信を失いやすい
特に小5の秋以降は、文章題や図形など“考える力”が求められ始め、差がつきやすくなります。
📈 理想的な学びの流れとは?
- 小5春〜夏:計算力をしっかり定着させる
- 小5秋〜小6:考える力を伸ばす問題に取り組む
- 小6:中学を見据えた“応用力”と“自信”を育てる時期
この流れに乗れた子は、中学入学後の学習もスムーズに進んでいきます。
🧠 子どもは“ポジション”に影響されて育つ
ここは、ぜひ保護者の皆さまに知っていただきたい大切なポイントです。
小学校高学年になると、子ども同士の中で自然に「○○くんは頭がいい」「私は△△さんより上」とか「下」とかいった学力のポジション意識が生まれます。
そしてその結果、やがて――
- 上の子は“上の子のふるまい”をしはじめ
- 下の子は“下の子の自信のない行動”をとるようになる
という、実際の行動や意識にまで影響するようになります。
🎁 今こそ、“良いポジション”をとる最大のチャンス
この時期に、「できた!」「わかった!」「褒められた!」という経験をたくさん積むことで、
お子さまは、クラスの中でも前向きな立ち位置をとることができます。
それは、
「勉強が得意になった」ということ以上に、これからの人生に大きな自信を与えてくれます。
🏫 マックスでの学びが、お子さまの未来を変える
マックスでは、「できる子のサイクル」に乗せるための仕組みを、日々の授業に取り入れています。
実際に――
「入塾したときは“算数がニガテ”と言っていた子が、半年後には“テストで満点とれた!”と笑顔で報告してくれた」
そんな場面が、毎年のようにあります。
🍀 ご家庭でできる、ちょっとした応援
「大きなこと」をする必要はありません。
たとえば、
- 「そのやり方、工夫してていいね」
- 「自分から勉強始めてるの、すごいね」
- 「今週のプリント、全部できたって聞いたよ。がんばったね」
そんなひと言が、お子さまにとって大きな自信の種になります。
✨ 最後に:今の小6は、もう“スタートライン”に立っています
小6の春は、「まだ小学生」ではなく、
「中学準備のスタートライン」です。
この時期に、どんな経験をするかで、
中学での学び方・意欲・そして自信が大きく変わります。
マックスでは、学力だけでなく、「自信」も育てていくことを大切にしています。
一緒に、お子さまの“最良のスタート”を応援させてください。
✅ 小6の春にやるべきことリスト(家庭用チェックリスト)
| 項目 | チェック欄 | 備考 |
|---|
| □ 計算ミスを減らす練習(筆算・暗算の反復) | | 1日5分でもOK、継続が大切 |
| □ 文章題に取り組む(式の立て方を確認) | | 考え方を「言葉」で説明する練習も◎ |
| □ 分数・小数の理解を整理し直す | | 苦手になりやすいポイントです |
| □ 国語の読解問題を1日1題ペースで読む | | 内容の要点をまとめる力を育てる |
| □ 書き写し・音読など、集中力を養う作業を取り入れる | | 朝や寝る前に3分だけでも効果大 |
| □ 苦手な単元をあいまいにせず、解き直しする | | 「わからないままにしない」を大切に |
| □ 家庭学習の記録を残す(簡単な日記でもOK) | | 自分で「やった!」と振り返る習慣に |
| □ 褒められる体験を意識して増やす | | 正解・チャレンジ・姿勢など全て対象 |
💬 家庭でできる“声かけ例”集
子どものやる気を引き出すには、シンプルで前向きな言葉が最も効果的です。
🔹「行動」に注目した声かけ
- 「自分から机に向かっててすごいね」
- 「今日やることを自分で決めたの?それは大人だね」
🔹「過程」に注目した声かけ
- 「途中であきらめずに考えてたの、見てたよ」
- 「間違っても、ちゃんとやり直しててえらい」
🔹「努力の継続」に注目した声かけ
- 「毎日少しずつ続けてるの、ほんとにすごい」
- 「昨日より今日、ちょっと早く終わったね!」
🔹「結果」に対する前向きな反応
- 「間違えたって、チャレンジしたのはかっこいいよ」
- 「できた!って顔が最高だったね」
◆鶴ヶ谷教室 ☎252-0998 989-0824 宮城野区鶴ヶ谷4-3-1
◆幸 町 教室 ☎295-3303 983-0836 宮城野区幸町3-4-19
◆マックス動画教室
電話でのお問合せ AM10:30~PM22:30
小5の冬以降は、学年を超える
春の集中授業の間は、いろいろな学年の子が、同じ時間帯に来ていますので、よくこんなことが起きます。
先生: 20分を時間にすると何時間だ?
中3A: 0.2時間です。
先生: そうか? その考え方で行くと、60分は0.6時間になってしまうぞ。
中3A: エ~? 20分は0.2時間じゃないんだ。
先生: Bさんはどうだ?
中3B: 習ってません。
先生: 本当? 小学校で、絶対に習っているよ。
中3B: 小学校で、そんなことやってませんよ。
先生: じゃ、向こうに小6の子が、来ているから聞いてみよう。オ~イ、Cちゃん。問題解いているときにゴメン。20分って何時間だ?
小6C: エッ? 20分ですか。(ノートに何か書いてから)3分の1時間です。
先生: ハイ。OK。 正解です。
中3B: エ――――エ。
中3A: スゲ~。
先生: Cちゃん。自分の問題に戻っていいよ。ありがとうね。ほら、3年生のみんな。小6の子が、できるぞ。
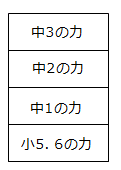
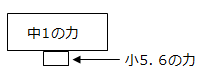
こんなことが日常的に起こっています。数学の土台の力は、小5~小6の算数の力です。でも、中学生になったからと言って、自然にできるようになったりはしないのです。むしろ小さい土台の上には、大きなものが乗らないので、やってやってもうまくいかない場合の方が多いものです。図にするとこんな感じです。
小5.6の力が大きい場合
小5.6の力が小さい場合
例えば、頑張って一瞬、こんな形になったとしても
時間が経つと、崩れて、結局は、こんな形になってしまう。
結果として見ると、我慢してやっても、最終的には報われず、「やってもダメだった」という一番、子どもが傷つく結果に終わりがちです。
できる中学生・高校生たちの共通点
成績のいい中学生・高校生たちには、共通点があります。頭がいいことではありません。
「自分はできる」と思っていることです。
まぁ、実際できるわけですが、不思議に「自分はできない」と思っている成績のいい子はいません。なぜでしょう? 彼らは小学校高学年の頃、勉強で先生から褒められる、お友達から「できる」と思われるという経験をたくさん積んで、「自分はできる」と思うようになったのです。
「自分はできる」と思っている子は、勉強があまり「苦痛」ではありません。体験的にいい思いができることを知っているからです。 だから、実際に勉強する時間も、他の子より自然に多いので、また次の「よい成績」と「高い評価」を手にするのです。下図のような「できる子のサイクル」に乗っています
。 
「できる子のサイクル」に乗せる
「褒められた」経験や「認められた」経験を、数多く体験させることを意図的に増やしていく。
そのためには、科目の特性や学習内容の進行具合、子どもの意識や子どもの精神的な成長段階、さらには子ども間の序列化の問題を理解しておくことが必要です。
科目の面からは、一般的に、小学生段階では、算数ができる子=頭がいい子と認識されます。算数が得意な子ほど、みんなから一目置かれるのが早いのです。 逆に算数ができない子は、他の科目ができない子より簡単に自信を失う傾向にあります。科目的には、まず算数の出来不出来が子どもの意識に影響します。
学習内容の進行具合からは、算数が、本格的に難しくなるのは、つまり、文章問題などの考える力が問題になるのは、小5の秋からです。 ということは、小5の春ぐらいまでは、計算力を徹底して鍛える。夏ぐらいから、考える力を鍛える問題に以降していくことが理想的なプログラムです。
精神的な成長段階・心の状態からは(是非とも、留意して戴きたい点です)、小学生も高学年になると「○○さんは私よりできる」とか「ボクは○○君よりできる」などと子どもたちの間で序列化が始まります。
この序列は、 当初は能力を反映したのもではない。
ところが、一般的に、序列ができてしまうと、不思議なもので、子どもたちは、序列に従って行動するようになります。
上位に位置取りした子は、上の子の行動をし始め、次第に本当に上の子に変わっていきます。下位に位置取りした子は、本人に能力があっても、やはり不思議なことに、下の子の行動・意識になっていきます。
このような実態を見ていると、本人が自我に目覚めた頃、どのポジションにいたかと言うことが、その子の先々まで、大きく影響していることに気が付きます。 わが子が、クラスの中でどのようなポジションにいるのかは、子どもの将来にとても大きなウエイトを占める問題ですし、子育ての苦労にもかかわる問題になります。
子どもの成長段階を考えると、今まさにそのど真ん中にいる訳です。子どもを「かわいそう」にしないために、今のうちに、少しでもいいポジションをとれるようにしてあげる。親がしてあげられる子どもへの大きなプレゼントになります。
伸びていく子の算数教室
小学生~高校生までを教えているからわかる考える力を伸ばす算数のポイント・ずっと伸びていけるポイントをご説明します。
円の面積
まずは、公式を確実に覚えます:円の面積=半径×半径×3.14
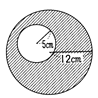
問題 : 図のしゃ線部分の面積を求めなさい。
初歩の段階から、「今、何をしているのか」を明確にするための言葉の式を作る。
ノートの例
(しゃ線部分の面積)=(大きい円の面積)-(小さい円の面積)だから、
12×12×3.14-5×5×3.14 =452.16-78.5 =373.66
答 373.66cm2
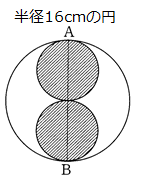
問題 : 図のしゃ線部分の面積はしゃ線のついていない部分の面積の何倍ですか。
ノートの例
しゃ線部分の面積=半径8cmの円が2つ 8×8×3.14×2……①
しゃ線のついていない部分の面積
(半径16cmの円)-(半径8cmの円2つ) =16×16×3.14-8×8×3.14×2
①と②をそれぞれ計算すると、両方とも401.92となり1倍となります。
これで満足しないでください。伸びる子は、力まかせに計算したりしません。単純計算の力=算数の力は、小5の夏までで終了しています。 3.14の計算を何回もするのは大変です。しかも間違いやすい。だから、計算回数を減らす工夫を考えます。
16×16×3.14-8×8×3.14×2
=16×16×3.14-8×16×3.14 となるので、
=16×16×3.14-8×16×3.14
=(16-8)×16×3.14 となります。さらに、
=8×16×3.14
=8×8×2×3.14……②となります。
①②どちらも、8×8×3.14×2だから①と②は同じ面積になる。よって 1倍
★×3.14の計算を1回もしないで、答えが求められました。 もともと「何倍ですか」と質問しているので×3.14の計算を何度もすることを求めて訳ではないのです。
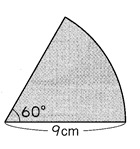
扇形の面積
不思議です。この時期こまでに、整数×分数の計算を習っていません。次の章で習います。正直に言って、教科書の章立てが悪いと思います。
では、どうするか。この段階で、パスするのも手だと思います。 整数×分数、整数÷分数を学習した後で、戻って学習する方がいいと思います。
そうは言っても、学校でテストもありますので、ここでは、一応は教科書に従います。 60°は円(360°)の6等分なので、この扇形の面積も円の面積の6等分だから、 9×9×3.14÷6=42.39㎝2
<本当に疑問です。こんな方法でいいのでしょうか? 例えば、中心角が50°のときは、どうするの?>
やはり、整数×分数、整数÷分数を学習した後で、もう1度、戻って改めてやり直すことにします。
◆鶴ヶ谷教室 ☎252-0998 989-0824 宮城野区鶴ヶ谷4-3-1
◆幸 町 教室 ☎295-3303 983-0836 宮城野区幸町3-4-19
◆マックス動画教室
電話でのお問合せ AM10:30~PM22:30