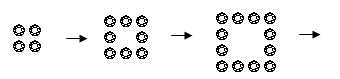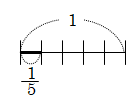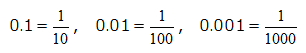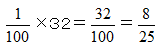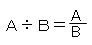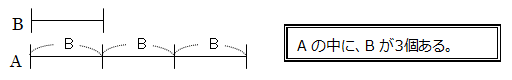やめる？続ける？お子さんの未来を変える習い事のやめどき　小５　１１月

習い事のやめ方は慎重に

今回は習い事についてです。

まず、２つに分けて考えてください。「短期の習い事」か「長期の習い事」かです。

「短期の習い事」は、数ヶ月～２年間といった短い期間で考え、目標を達成した時点で終了します。 一方、「長期の習い事」は、大きな目標を長い期間かけて達成するために続ける習い事です。継続することを前提に始めることになります。

仮にスイミングの場合で考えてみましょう。「２５m泳げるようになる」という目標の方は、「短期の習い事」です。「将来、水泳の選手を目指す」という目標の方は、「長期の習い事」になるわけです。

また、「中学校に入るまでの基礎体力づくり」であれば「短期」、「健康のため続けさせる」のなら「長期」となります。

習い事は、目指すものによって、その期間が変わってきます。「短期の習い事」の方は、目標を達成した時点で、辞めるか続けるか見直しが必要です。今回、特に取り上げたいのは、この辞め方です。

目標が達成できたからやめる。これが一番いい辞め方です。期間がきたからやめる。これもなかなかいい辞め方です。 面白くなくなったからやめる。辛いから辞める。問題はコレです。

ご両親としては、大人として妥当な判断を下された事だと思います。しかし、子どもが、それをどう解釈したのか、そこから何を学んだのかは、ご両親の判断とはまったく別物である場合が多いのです。

例えば、ピアノを習っていた。子どもがやりたいと言い出したので始めた。しばらくやらせたが、才能があるわけではなし、 長期的な目的があったわけでもない。最近、子どももやる気はないようだし、このあたりで辞めようか。

子どもは何を学んだのか？

大人としては、妥当な判断です。しかし、子どもの理解は、別の所にあります。

もしかすると、子どもは、面白くなくなったら辞めてもいいんだ。辛くなったら辞めてもいいんだということを 学んでしまったかも知れません。

ご両親の判断は、間違っていません。しかし、子どもには、どう伝わったでしょうか。子どもには子どもの解釈があります。

中３生で、受験期の一番辛い秋ごろに、投げ出してしまう子に、このような経験を持っている子が多くいます。あえて醒めた言い方をさせて頂くなら、そのように育てたと言えます。

だから、「短期の習い事」は、始める時に、「目標」や、「期間」をハッキリさせておくことが賢明です。今、習い事をしているけど、そもそも目標なんてなかったと言う方は、今からでも「目標」や「期間」を設定することをお勧めします。

そうしておけば、「面白くないから辞めたい」、反対に「楽しくてやめたくない」のどちらの場合にも適切に判断が下せます。「楽しくてやめたくない」は、何も問題なさそうですが、数ヶ月後に、楽しくなくなったら・・・

「おもしろくないから辞める」それも一つの考え方です。私も根性とか根気などと言うよりも、「おもしろくなかったら辞める」が自然な感じがしていました。

しかし、この立場をとると将来　別な問題を抱え込みます。それは、子どもに理解できるように、ピアノと受験の違いを説明できるかという問題です。

高校受験の時に、「おもしろくないから辞める」に対して、「受験には一生がかかっている」と説明しても、子どもには通用しません。世の中のことをあまりに知らないからです。それは、目的もなしに高校を中退する子の多さなどにも現れています。

「そんなこと、ひとりでにわかるだろ」とおっしゃる方もいます。でも、子ども側から見れば、「そんなの大人の勝手」としか見えないのです。

習い事は、目的や期間をきめてから

そういう意味でも、「目的」や「期間」を予め設定した習い事をお勧めします。一事が万事です。

小学生～高校生までを教えているからわかる、考える力を伸ばす算数のポイント・ずっと伸びていけるポイント。

きまりを見つけて

問題：図のように、おはじきを正方形の形にならべます。１辺が１０このとき、まわりは何こですか。

対応表を作ります。 （上段）１辺のおはじきの数　（下段）まわりの数です。

対応表を見て考えます。 （上段）の１辺のおはじきの数が1つ増えると、 （下段）のまわりの数はいくつ増えますか。 そうです。４つ増えますね。じゃ、対応表の続きを書いていきましょう。

小学生～高校生までを教えているからわかる、考える力を伸ばす算数のポイント・ずっと伸びていけるポイント。

分数と小数

分数って、「便利な数」だと思うようになれば、間違いなく数学は得意科目になります。逆に分数を「変な数」と思っていると、将来に禍根を残します。

１÷３で、「わり切れません」と言うようなら、かなり危ない状況です。

問題：「1/5 を小数にしなさい」

分数を小数に変換する場合は、（分子）÷（分母）。よって １÷５＝０.２

ただ（分子）÷（分母）と覚えるだけでなく、考え方を組み立てられることが大切です。

・線の太い部分は、全体の１を５個に分けたうちの１個分だから、1/5

・１を５つに分けたら１つの大きさは、１÷５＝０.２

この２つは同じ大きさだから、1/5 ＝１÷５＝０.２

問題：「０．３２を分数にしなさい」

小数を分数に変換するには、

を使います。

０.３２は０.０１が３２個だから、

迷ったら試してみる。 試せることが高い学力の証拠

と覚えればいいのですが、４÷５が　4/5　か　5/4　か迷った時にどうするか？

次のように【試し】てみればいいのです。

割り切れる１０÷２で、５になるのが　　10/2　か　2/10 かを確認する。

このような簡単なチェックをなにげなくできるようになっていれば、高い学力を獲得してきていると見て間違いありません。

小学生～高校生までを教えているからわかる、考える力を伸ばす算数のポイント・ずっと伸びていけるポイント。

分数倍

「１０は５の何倍ですか」という問題に苦しむ子はそうそういません。しかし、数字が反対になり「５は１０の何倍ですか」となると話は、違ってきます。

さらに「３は１０の何倍か」となるといよいよ大問題です。

学習のポイント：分数倍でも、整数倍と同じように、考えればいいことを腑に落ちるまでやる。

腑に落ちる前に止めてしまうと、「分数は変な数」と認識する子になってしまう。 確かに、３倍はイメージできても、4/5 倍はイメージしにくいでよう。

線分図を書いて、見えるようにします。

線分図　AはBの３倍。　「３倍」　＝　Bの３個分

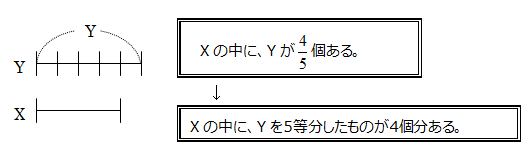
線分図　XはYの4/5倍。　「4/5倍」＝　Yの4/5個分

２倍、３倍・・・はイメージ的にも簡単です。整数倍から線分図を書く練習をして、分数倍に入ります。

分数倍で、「 個分」が初めピンと来ないときは、「５等分したものが４個分」でもOKです。「倍」って、いつも大きくなるとは限らないという発見もあります。

自分で、線分図を書けるようになる事が、理解を深める大きなポイントです。書いてもらった線分図を見て、「わかる」段階で終了にしないでください。

小学生～高校生までを教えているからわかる、考える力を伸ばす算数のポイント・ずっと伸びていけるポイント。

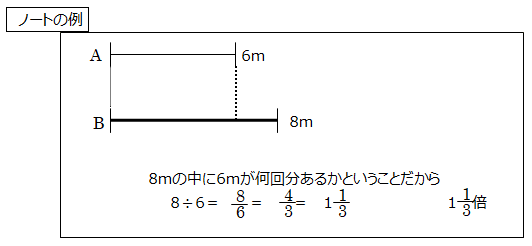
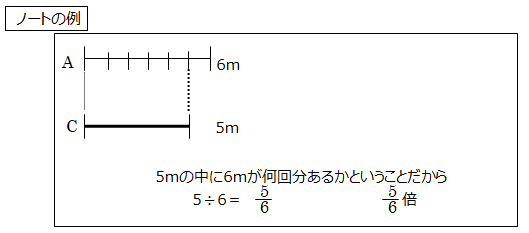
問題：　紙テープＡの長さは６m,紙テープＢは８m,紙テープＣは５mです。紙テープＡの長さをもとにすると,紙テープＢと紙テープＣの長さはそれぞれ何倍ですか。

「紙テープＡをもとにすると、紙テープＢは何倍か」とは、簡単に言うと、紙テープＢの中に、紙テープＡが何個分ありますかということ。

「紙テープＡをもとにすると、紙テープCは何倍か」とは、簡単に言うと、紙テープCの中に、紙テープＡが何個分ありますかということ。

「割合」「百分率」の章でもっと掘り下げます。ここでは、「わり算と分数」がテーマなので、わり算の意味を中心に教えます。

わり算の意味について一言。

１０÷２は、だれでも５と正解しますが、意味は？と聞かれると「？」の子がたくさんいます。

意味は２つあります。①１０を２つに分ける。　②１０の中に２は何個あるか。

②がなかなか出てきません。しかし、問題を解くときには、②の考え方の方がよく使いますし、重要です。

また、②の考え方を使うと、1/2÷1/2 が１になることも簡単に説明できます。

さらに、分速200ｍで、1000ｍ進むときにかかる時間はでも、公式を使わずに、1000ｍの中に1分で進む200ｍが5回あるから、5分と自然に解答できます。

小学生～高校生までを教えているからわかる、考える力を伸ばす算数のポイント・ずっと伸びていけるポイント。

図形の角

ひと休み的な簡単な単元です。 学習のポイント

①三角形の内角の和は１８０°を覚える。 ② 多角形は図をかいて、三角形に区切って考える。

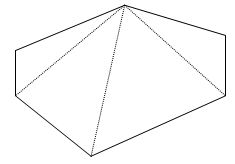
「三角形の３つの角の和は１８０度」であることを覚えます。多角形の場合は、公式もありますが、５年生では公式によらず、対角線を引いて多角形をいくつかの三角形に分割して角の和を求めます。

左の六角形は、対角線で４つの三角形に分かれるから、
６つの角の和は、１８０°×４＝７２０° で、７２０°になる。

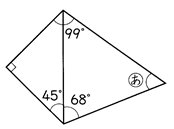
問題：次の図で「あ」の角度を求めましょう。

ノートの例：

四角形の４つの角の大きさの和は３６０°だから
３６０－（９９＋９０＋４５＋６８） ＝３６０－３０２ ＝５８　　答　５８°