小5生 保護者の皆さまへ
「割合」が未来を切り開く鍵 – 基礎からじっくり学ぶ重要性
なぜ「割合」が重要なのか?
現在、学校で「割合」の単元に取り組んでいるお子さまも多いかと思います。この単元は、単なる算数の一部ではなく、中学以降の数学の基盤となる重要な内容です。将来の数学や理科の成績にも直結するため、正確に理解しておくことが必要です。
しかし、学校の授業は1か月程度で次の単元へ進むため、多くのお子さまが「理解しきれないまま次に進む」という課題を抱えています。実際、「割合を自由自在に操れる中学生」はほんの一握りというのが現実です。
「割合」を学ぶことで得られる力
1. 中学数学へのスムーズな移行
中学では、算数的な計算から数学的な考え方へと移行します。「割合」をマスターすることで、文字式や方程式を扱う基礎が身につきます。
2. 日常生活で役立つ計算力
買い物や仕事など、割合の計算は実生活でも頻繁に使います。例えば、「100円の20%引きはいくら?」といった場面で役立つ力です。
3. 考える力の土台を作る
「筋道を立てて考える力」が育まれます。これは、抽象的な学びが増える中学以降でも非常に重要なスキルです。
具体的な学びのステップ
割合の理解を深めるためには、基本的な計算から応用問題まで段階的に学ぶ必要があります。以下のようなステップで進むことをお勧めします。
レベル① 基本形を理解する
「520gは400gの何%ですか?」
まずは、割合の基本形である「●は◆の何%ですか?」を正確に解けるようにします。
レベル② 文を正確に読み解く
「学校の6年生175人のうち、女子は91人。女子は全体の何%ですか?」
文の内容を正確に理解し、「●は◆の何%ですか?」に落とし込む練習をします。
レベル③ 実生活の問題に挑戦する
「800円の20%引きはいくら?」
中学でも通用する考え方(例:80%=100%-20%)で進めたいと思います。
だから、「800円の20%引き」は、100%-20%=80%で、「800円の80%」と考えます。「a円のx%引き」は、100%-x%=(100-x)%で、「a円の(100-x)%」と対応できるようにしておくと中学にスムーズにつながります。
レベル④ 複数の割合を使う問題を解く
「敷地面積の20%が庭で、その10%が池。池の面積は3.2㎡。敷地面積は何㎡?」
基本形を繰り返し使うことで、複雑な問題にも対応できる力を養います。
レベル⑤ 線分図を活用して考える
「62人のメガネをかけている生徒は全体の10%より6人多い。全校生徒は何人ですか?」
問題の状況を視覚的に整理する技術を学びます。
問題が意図していることを理解するために 図を描きます。 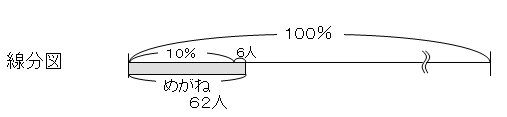
上記のような線分図が描ければ、 62-6=56人が、 全体の10%だと気がつきます。 すると、「全校生の10%は56人です」と ①レベルの問題になりました。
保護者ができるサポート
お子さまが「割合」を理解するためには、学校での短期間の学習だけでは足りません。次のようなサポートを意識してみてください。
1. 繰り返し練習の場を作る
割合の理解には反復が必要です。同じ問題を何度も解くことで、確実に身につきます。
2. 筋道立てて考える癖をつける
「なぜこの計算になるのか?」を一緒に考える時間を持つことで、計算の背景を理解させることができます。
3. 焦らずじっくり取り組む
割合は一朝一夕で身につくものではありません。長い目で見て学習をサポートすることが大切です。
最後に
小学校高学年は、学習内容が具体的なものから抽象的なものへと大きく変わる時期です。「割合」をはじめとする基礎的な内容を確実に身につけることで、中学以降の学習が大きく変わります。
私たちMaxでは、お子さま一人ひとりのペースに合わせて学びをサポートしています。この時期にしっかりと基礎を固め、未来へのステップを一緒に築き上げていきましょう。お気軽にご相談ください!

◆鶴ヶ谷教室 ☎252-0998 989-0824 宮城野区鶴ヶ谷4-3-1
◆幸 町 教室 ☎295-3303 983-0836 宮城野区幸町3-4-19
電話でのお問合せ AM10:30~PM22:30

