【小5保護者様へ】算数の最大の山場「割合」。
つまずく子と伸びる子を分けるのは「〇〇化」の習慣でした。
保護者の皆様
あけましておめでとうございます。
新しい年、2026年が始まりました。
小学校生活も後半戦。
5年生の冬は、算数において「6年間で最も重要な分岐点」と言われています。
この1月から春にかけて、「あれ? 急に算数が難しくなったかも…」とお子様の表情が曇る瞬間があれば、
その正体は十中八九、これです。
算数の最難関単元、「割合(わりあい)」です。
今日は、多くのご家庭を悩ませるこの「割合」について、
- なぜ、急にできなくなるのか?
- 苦手にしないための「たった一つの習慣」とは?
- 中学数学へどうつながるのか?
現場で実際に見てきた事実をもとに、お話しします。
なぜ「割合」は、こんなに難しいのか?
「100円の2倍は?」
「50%オフって半分だよね?」
ここまでは、感覚的にほとんどの子がスラスラ答えられます。
しかし、
「250円の2割引きはいくら?」
「定価の80%で売ったら利益が〜」
という問題になった途端、ピタリと手が止まります。
これは、能力の問題ではありません。
「思考の質」が変わったからです。
これまでの算数は「リンゴが何個」という「具体的な数」でした。
しかし割合は、「Aを1としたとき、Bはいくつか」という「関係性(抽象的な概念)」を問われます。
つまり、小学校で初めてぶつかる
👉 「構造を理解しないと、公式を覚えても解けない単元」
なのです。
だからこそ、つまずくのは自然なこと。
焦る必要はありません。
【実話】「意味わかんない」と言ったAくんの変化
昨年、5年生のAくんは「割合」の授業中、鉛筆を置いてこう言いました。
「先生、計算はできるけど、意味わかんない。つまんない」
「くもわ(比べ・もと・割合)」の公式を丸暗記しようとして、パンクしていたのです。
そこで私たちが徹底したのは、「すぐに式を作らせないこと」でした。
- 簡単な図を描いてみる
- 「どっちが基準(もと)かな?」と言葉にする
- 正解よりも「図の描き方」を褒める
これを繰り返したある日、Aくんがポツリと言いました。
「あ、これって結局、“どれを元にしてるか”ってだけの話か」
この「言語化」ができた瞬間から、彼の算数は劇的に伸びました。
春には「割合、パズルみたいで面白いかも」と笑っていました。
マックスが「割合」を絶対に急がない理由
合格屋マックスでは、割合の単元にじっくりと時間をかけます。
理由は一つ。
👉 割合は「慣れ」と「言語化」が命だから。
いきなり公式を暗記させると、その場は解けても、文章が少し変わっただけで解けなくなります。
遠回りに見えても、「なぜそうなるか」を自分の言葉で説明できるまで待つ。
この粘り強さが、
- 6年生の「速さ・比」
- 中学理科の「濃度・密度」
- 中学数学の「方程式の文章問題」
へつながる最強の土台になります。
ご家庭でできる!一番効果的な「魔法の習慣」
ここで、保護者の皆様に一つだけお願いがあります。
👉 お家では、勉強を教えなくて大丈夫です。
(親御さんが教えると、解き方の違いでケンカになりがちです!)
その代わり、「スーパーマーケット」を教室にしてください。
お買い物の時、「20%引き」のシールを見つけたら、
「これ、いくらになると思う?」とクイズを出してみてください。
「えーっと、10%がこれくらいだから…」
と、頭の中でイメージする。
この「感覚としての割合」を養うことが、机の上の勉強より何倍も効果的です。
【よくあるご質問】小5・割合Q&A
12月の面談で多かったご質問にお答えします。
Q. 家庭で毎日、割合のドリルをやらせるべきですか?
A. 量より質です。毎日でなくて大丈夫です。
大量の問題をこなすより、1問に対して「どうしてこの式になったの?」と聞いてあげてください。説明しようとすることで、脳が整理されます。
Q. 計算はできるのに、文章題になると止まります。
A. 正常な反応です。
文章題こそが「割合」の本質です。「止まっている時間」は「考えている時間」。すぐに教えず、見守ってあげてください。
Q. 親が教えた方が早い気がします…
A. グッとこらえて、「質問」に徹してください。
「答え」を教えるより、「どこまで分かったの?」と聞いてあげるほうが、お子様の力は長く伸びます。
最後に:保護者の皆様へ
「今は分かっていない」
それは、決してマイナスではありません。
「今まさに、抽象的な思考の階段を登ろうとしているサイン」です。
私たちは、目先のテストの点数だけでなく、
その先の中学・高校入試まで見据えて、
この「割合」という山場を一緒に登り切ります。
「この塾で、割合をやっておいてよかった」
そう言っていただける自信があります。
どうぞ、安心してお任せください。
本年もよろしくお願いいたします。
ご家庭用 算数のポイント
算数教室 割合
算数教室 三角形・平行四辺形の面積
◆鶴ヶ谷教室 ☎252-0998 989-0824 宮城野区鶴ヶ谷4-3-1
◆幸 町 教室 ☎295-3303 983-0836 宮城野区幸町3-4-19
電話でのお問合せ AM10:30~PM22:30
割合

まず、導入時期は、形で処理できるようにします。

解き方の手順
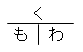
① 問題文の中から「わ」(割合)を見つける。割合は~倍,~%,~割,単位のない数
② 問題文の中から「も」(もとにする量)を見つける。もとにする量は問題文の中で割合の前の「の」の前にある
③ 問題文の中から「く」(くらべられる量)を見つける。問題文の中で残っている数がくらべられる量。
「もとにする量」と「くらべられる量」は同じ単位なので、もとにする量の発見が重要。
④ 数字で分かった2カ所を  に代入して計算する。
に代入して計算する。
問題 : 「4mは9mの何倍ですか。」
考え方
① 問題文の中から「割合」を見つける ⇒⇒倍がついている「何倍」
② 問題文の中から「もとにする量」を見つける。 ⇒⇒問題文の中で割合の前の「の」の前にあるのは「9m」
③ 問題文の中から「くらべられる量」を見つける ⇒⇒残っているのは「4m」
④ 数字で分かった2カ所を  に代入する。
に代入する。
「割合」を求めるには、横棒だからわり算をする。 4÷9= ←←← わり算は分数にする。
←←← わり算は分数にする。
子どものノートの例

上記のノートの例のように、式と答えだけでなく、「わ」(割合)、「も」(もにする量)、「く」(くべられる量)をチェックして、すべてをノートに書き出します。
問題を読んだら、無意識に「わ」、「も」、「く」をチェックすることが基本です。 最初から徹底して基本にこだわっていくことが何より大切です。「難しくなったらやる」と言いますが、普段からやっていないと、イザ、本当に難しくなった時に、手に技術がついてなくて使えないから、「難しくなったらやる」は、現実的にはアウトです。
百分率や歩合を  に入れる時は、「割合」を 小数か分数にします。この部分は、下の表を覚えれば、
に入れる時は、「割合」を 小数か分数にします。この部分は、下の表を覚えれば、
簡単です。
1%=0.01 1割=0.1 10%=0.1 1分=0.01 100%=1 1厘=0.001
1題1題、めんどくさがらずに、自然に頭が働くようになるまで ノートに必ず「わ」、「も」、「く」を書き出してから、式を立てます。
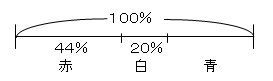
問題: みち子さんは色紙を75枚持っています。そのうち赤い色紙は33枚で、白い紙は全体の20%にあたります。残りは青い色紙だそうです。
(1)赤い色紙は全体の何%にあたりますか。
(2)青い色紙は何枚ありますか。
基本型「~は-の□%」で考えます。
(1) 赤い色紙は33枚、全体は75枚、だから「33枚は75枚の何%」かということ。
「わ」:何%、 「も」:75枚、 「く」:33枚 だから 33÷75=0.44 (答)44%
(2)赤が全体の44%、白が全体の20%だから、青は、100-(44+20)=36%
「青い色紙は全体の36%」だから 75×0.36=27 答) 27まい
中学・高校で使える割合の力を獲得するために、小5の後半にはマスターしたい問題の例。

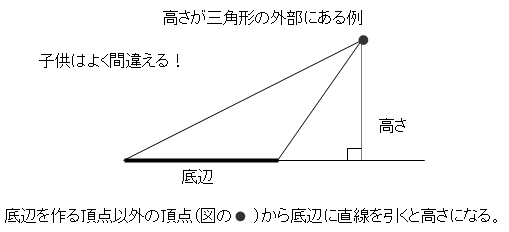
平行四辺形と三角形の面積

① 公式を覚える。
② ノートに図を書き写して「底辺」「高さ」が垂直に交わる所を確認する。

底辺と高さが直交しているかどうかを確かめないまま、
問題に出ている2つの数を公式に入れて計算する子がいます。
多角形の面積は、三角形や四角形の面積を組み合わせます。
ノートに図を書いて、いろいろな線を引いてみて三角形や四角形に分けてみます。
この際にもノートに図を書き写して、「底辺」と「高さ」が直交しているかのチェックが必要です。
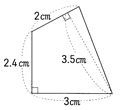
問題 : 図の四角形の面積を求めなさい。

ノートの例
四角形を①②の二つの三角形に分ける。

①の三角形の面積 3×2.4÷2=3.6
②の三角形の面積 2×3.5÷2=3.5 よって四角形の面積は 3.6+3.5=7.1㎝2
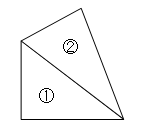
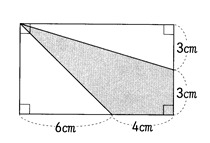
問題 : 次の色を付けた部分の面積は何㎝2か。

全体の四角形から①と②の三角形を引く。

別解 求める四角形の面積を①と②の三角形に分ける。

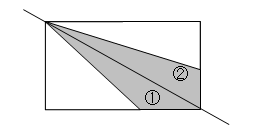
問題 : 次の色を付けた部分の面積は何㎝2か。

2つの三角形を合わせると三角形の底辺は平行四辺形の底辺と同じ。2つの三角形の高さは5cmで、同じだから新しい三角形の高さも5cm。

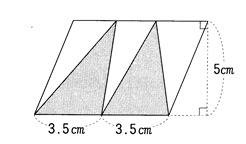
問題 : 次の色を付けた部分の面積は何㎝2か。
一見難しそうですが、上側の図のように2つの三角形(①,②)に分けると簡単に面積を求められます。 
小5保護者必見!算数「割合」克服のカギは〇〇だった!
新しい年が始まりました。お子様の小学校生活もいよいよ後半戦。高学年になり、学習内容も難しくなってきましたね。今年もお子さまの学びを全力でサポートしてまいりますので、どうぞよろしくお願いいたします。
さて、小学校算数の中でも特に重要で、そしてお子様にとって最初の大きな壁となる単元、「割合」に差し掛かる時期がやってきました。この単元をしっかり理解できるかどうかが、今後の算数・数学への自信と成績に大きく影響します。
「割合」って、なぜ難しいの?
「100円の2倍は何円ですか?」には簡単に答えられても、「298円の税込価格は何円ですか?」になると悩んでしまうお子様は少なくありません。これは、「割合」が、「もとにする量」(基準量)、「くらべる量」(比較量)、「割合」の関係性を理解する必要があるためです。
例えば、「100円の2割引」は計算できても、「250円の2割引」になると途端に難しく感じる子どもが多いのです。100円を基準とした場合、1割引は10円、2割引は20円とすぐに計算できますが、250円を基準とした場合は、1割引を計算するために250×0.1をする必要があり、ここでつまずいてしまうのです。
小学校の授業だけでは時間が足りない!
「割合」という単元は、理解を深めるには、時間をかけてじっくり取り組む必要があります。しかし、学校の授業時間は限られており、十分な練習時間を確保することが難しいのが現状です。
そこで、家庭学習や塾での学習が重要になります。
マックスの取り組み:お子様に「割合」を好きになってもらう!
マックスでは、1月から夏前までの期間、「割合」の理解を深めるための特別なプログラムを用意しています。
- 繰り返しの徹底: 毎回の小テストで理解度をチェックし、繰り返し学習することで、確実に定着させます。つまずきやすいポイントを何度も復習することで、苦手意識を克服できます。
- 個別対応で苦手をフォロー: 一人ひとりの理解度に合わせて丁寧に指導し、「わからない」を「わかった!」に変えていきます。お子様がどこでつまずいているのかを的確に見極め、個別に最適な指導を行います。
- 実践的な問題で活用力を育成:「実際の買い物」や「レシピの分量変更」など、身近な例を通して、楽しく「割合」を学べる工夫をしています。算数が日常生活でどのように役立つのかを理解することで、学習意欲を高めます。
保護者の皆さまへのお願い
「割合」を克服するためには、家庭でのサポートも大きな力となります。ぜひ、お子様と一緒に「割合」に挑戦してみましょう!
- 一緒に問題を解いてみる
簡単な問題を親子で一緒に解き、「解けた!」という達成感を共有しましょう。
- 日常生活での会話に取り入れる
例:「この商品、30%引きだといくらになるかな?」といった日常の買い物を学びに繋げます。
- ポジティブな声かけをする
「少しずつ慣れてきたね!」「よく頑張ってる!」と努力を褒めることで、モチベーションを高めましょう。
- 家庭学習で役立つツールを活用する(別途リンク掲載予定)
おすすめのドリルやアプリなどを活用して、家庭学習を充実させましょう。
何かご質問やご不明な点がございましたら、お気軽にご相談ください。
お子様の「割合」の克服、そして算数が好きになるように、私たちと一緒に頑張りましょう!





 に代入して計算する。
に代入して計算する。