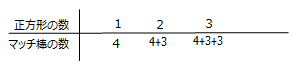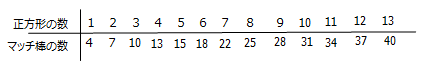こんにちは!
小4の12月に差し掛かると、算数を「嫌い」と感じ始めるお子さまが増えてきます。これまで好きだった算数が苦手に変わる大きな原因――それが「分数」です。
実は、この分数が今後の学力を大きく左右します。今回は、分数の重要性と、その克服方法について具体的にお伝えします。
1. なぜ分数が重要なのか?
理由1: 思考力が求められる単元
分数は、単純な計算だけではなく「理解力」や「思考力」が必要な単元です。
例えば、次のような内容があります:
- 仮分数と帯分数の変換
- 異なる分母の分数の大小比較
これらは「数の意味」をしっかり理解しないと解けないため、苦手意識を持つお子さまが増えるのです。
理由2: 5年生以降でのつまずきにつながる
分数は小4で基礎を学び、小5以降で応用問題が増えます。例えば、分数の加減・乗除計算や割合の問題など。
このとき、小4での練習が不足していると、「何をやっているのかわからない」という状態に陥ります。
よくある声
- 「分数って変な数!」
- 「どうしてこんな面倒な計算をするの?」
こうした苦手意識を防ぐためにも、今のうちに分数を得意にしておくことが必要不可欠です。
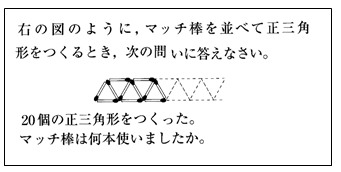
2. お子さまの分数理解度をチェック!
まずは、現在のお子さまの理解度を確認してみましょう。以下のテストを行うことで、どの程度分数を理解できているかが分かります。
テストA: 基礎チェック
- 内容: 仮分数・帯分数の変換や、分母が同じ分数の大小比較
- 目標: 13分以内に85点以上
- 結果:
- 85点以上:基礎は十分。応用力を伸ばす次のステップへ!
- 85点未満:冬休みに復習が必要です。
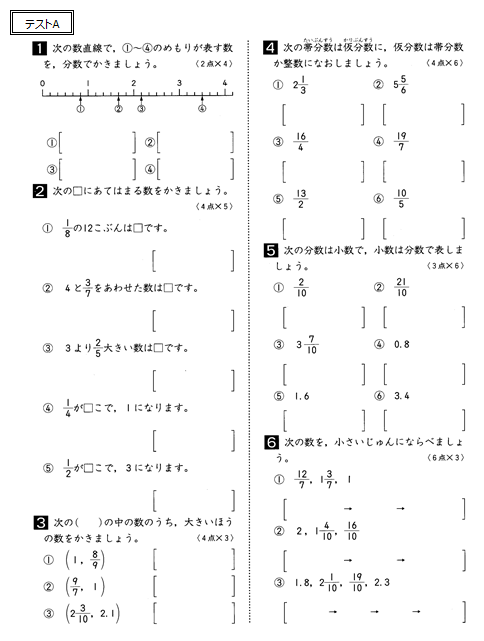
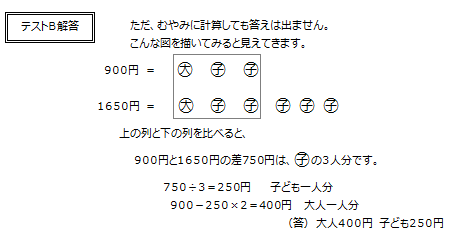
テストB: 思考力チェック
- 内容: 応用力を問う問題
- 目標: 問題を5分程度考え続けられるか
- 結果:
- 5分以上試行錯誤できる:思考力が育っています。応用練習を増やしましょう!
- 2~3分で諦める:さらなる思考力トレーニングが必要です。

3. 冬休みは分数克服の絶好の機会!
冬休みは、分数を徹底的に克服するための絶好のタイミングです。以下の方法でお子さまをサポートします。
取り組む内容
- 分数の基礎を徹底反復
- 仮分数や帯分数の変換を繰り返し練習して定着を図ります。
- 応用力を鍛える問題に挑戦
- 思考力を育てる問題に取り組み、試行錯誤する力を養います。
- 個別進捗レポートを保護者にお届け
- テストの結果や授業内容を保護者の方にフィードバックし、今後の対策をご提案します。
4. 分数の克服が未来の成績を左右する!
分数を自在に扱えるお子さまと、「分数は変な数」と認識してしまうお子さまでは、この先の学力に大きな差が生じます。この差は放置するとどんどん広がり、算数だけでなく中学以降の数学にも影響を及ぼします。
だからこそ、今がチャンス!
冬休みにしっかりと時間を取って分数を克服すれば、これからの算数の学習がスムーズになり、苦手意識を持たずに進めるようになります。
5. こんな方法もご活用ください
当塾では、分数の克服や学力向上のために、お子さま一人ひとりに合わせた指導プランをご用意しています。必要に応じて、特定の単元に絞った短期集中授業(週2回など)も可能です。
「うちの子の場合はどうすれば…?」といったご相談も、ぜひお気軽にお寄せください。
最後に:分数が未来を変える!
分数は、今後のお子さまの学力を左右する重要な単元です。冬休みという貴重な時間を活用して、「分かる」「できる」喜びを一緒に育てましょう。
この冬が、学力を飛躍させる第一歩となりますように――。
分数を得意にして、算数をもっと楽しく!ご相談をお待ちしています。
解答
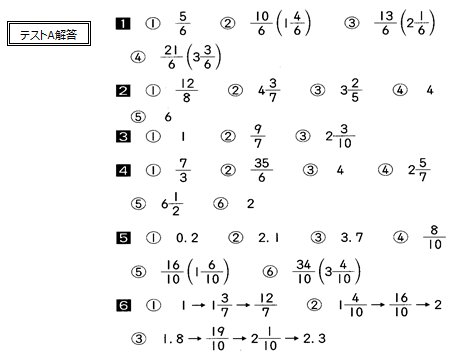
◆ よくあるご質問 Q&A(まとめ)
- Q1:小4のこの時期に分数でつまずくのは、やっぱり良くないでしょうか?
-
A:珍しいことではありませんので、必要以上に心配なさらなくて大丈夫です。ただ、今のつまずきを放置すると、小5以降の「割合」「分数の計算」「比例・反比例」などで困りやすくなります。
逆に言えば、小4の冬に一度立ち止まって分数を整理しておくと、その後の算数がとても楽になります。 - Q2:家ではどんなサポートをしてあげればいいですか?
-
A:まずは「わからないところがあっても大丈夫だよ」と安心させてあげることが一番大切です。そのうえで、
- 問題を一緒に読む
- 図や絵で一緒にイメージしてみる
- できたところをしっかりほめる
といった関わりが効果的です。
細かい解き方は塾に任せていただいて、ご家庭では“安心できる環境づくり”をお願いいたします。
- Q3:冬休み、分数の勉強はどれくらいの時間を目安にすればいいですか?
-
A:長時間の勉強は必要ありません。
1日15〜20分程度をコツコツ続けることが一番の近道です。
例としては、- 仮分数と帯分数の変換を5〜10分
- 分数の大小くらべを5〜10分
といった形で、「短く・毎日」を意識していただければ十分です。
- Q4:分数が苦手だと、この先どこまで影響しますか?
-
A:小学校のあいだは「何となく」で乗り切れてしまうこともありますが、中学以降の数学では分数の理解が土台になります。
方程式・関数・比例・反比例・確率など、ほとんどの単元で分数が出てくるからです。
だからこそ、小4の今のうちに「分数はこわくない」「意味がわかる」という感覚を持っておくことが、とても大きな安心材料になります。 - Q5:うちの子の状況について、個別に相談しても大丈夫ですか?
-
A:もちろん大歓迎です。
「テストではどこまでできていれば安心か」「この問題でつまずいているけれど、どう考えればいいのか」など、具体的な内容があればあるほどアドバイスしやすくなります。
お子さま一人ひとりの様子を見ながら、その子に合った分数の克服ステップをご提案いたしますので、どうぞ遠慮なくご相談ください。

◆鶴ヶ谷教室 ☎252-0998
989-0824 宮城野区鶴ヶ谷4-3-1
◆幸 町 教室 ☎295-3303
983-0836 宮城野区幸町3-4-19
電話でのお問合せ AM10:30~PM22:30