中学1年生で学ぶ平面図形。「2点から等しい距離にある点を見つける問題」や「直線と円の交点を求める問題」など、子どもたちからよく「これ、将来何の役に立つの?」と聞かれる単元です。
実は、この内容が身近な技術であるカーナビやスマホのGPSに役立っているとしたら、驚きませんか? 今日は、そんな数学の意外な活用法をお伝えします。
まずは基本の確認
数学の授業でこんな問題を解いたことはありませんか?
「点Aと点Bから等しい距離にある点を直線上で求めなさい。」
この問題は、2つの点から同じ距離にある場所を求める練習問題です。このとき、点Aと点Bを結ぶ直線の垂直二等分線が答えになります。
さらに発展させると、こんな問題があります。
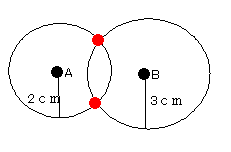
「点Aから半径2cm、点Bから半径3cmの円を描き、それらが交わる点を求めなさい。」
これも、平面図形で学ぶ基本的な考え方です。この2つの円が交わる場所が答えになります。
身近な応用:スピーカーを使った位置特定
では、これを日常生活に結びつけて考えてみましょう。
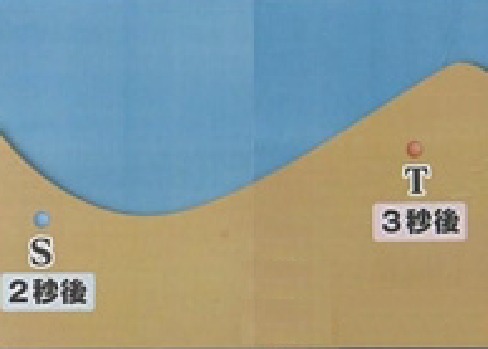
問題: 海辺にスピーカーSとスピーカーTがあります。それぞれが同時に音楽を流したとします。あなたがある地点にいるとき、Sからの音が届くまで2秒、Tからの音が届くまで3秒かかりました。音速を1秒あたり340mとすると、あなたはどこにいるでしょう?
解説:
- Sからの音が届くまでに2秒かかるので、Sからの距離は2 × 340 = 680m。
- Tからの音が届くまでに3秒かかるので、Tからの距離は3 × 340 = 1020m。
- Sを中心とした半径680mの円と、Tを中心とした半径1020mの円を描き、その交点が現在地です。
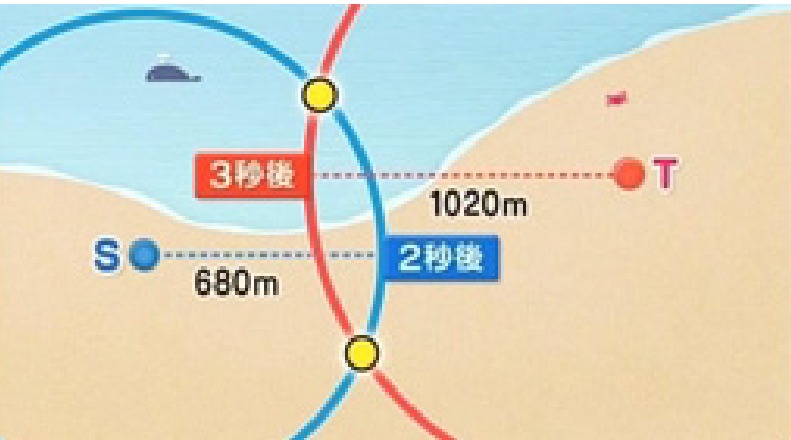
これが、GPSの基本的な仕組みと同じ考え方です。
カーナビの仕組み
カーナビやスマホに搭載されているGPS(Global Positioning System)は、地球を周回する複数の衛星から送られてくる電波を利用しています。この電波には、衛星が発信した正確な時刻情報が含まれています。
具体的な仕組み:
- GPS受信機は、電波が届くまでの時間を計測し、衛星までの距離を計算します。
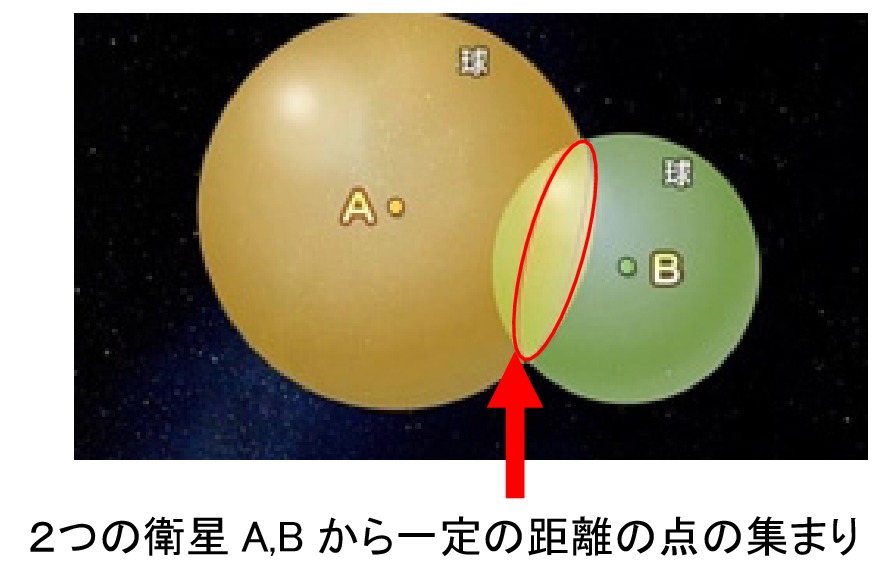
- 距離がわかると、衛星を中心とした球を描くことができます。
- 3つ以上の衛星を利用して、球同士の交点を求めることで、自分の現在地を特定します。
マックスの授業での取り組み
マックスでは、このような実生活での応用例を取り入れながら授業を行っています。
授業の一例:
- 作図の練習: 地図上に複数の点を設定し、コンパスや作図ソフトを使って等しい距離を描き、交点を求める。
- 計算の実践: スピーカーの問題を用いて、円の半径や交点を計算する。
- 発展学習: GPSの仕組みや人工衛星の役割について学び、図形の知識がどのように使われているかを深掘り。
数学が単なる学問ではなく、生活を支える技術に直結していることを実感できます。
子どもたちの反応
実際に授業でこの話をすると、子どもたちからはこんな感想が寄せられます。
- 「カーナビってこんな仕組みだったんだ!」
- 「数学ってやっぱり役に立つんですね!」
- 「もっといろんな技術に数学が使われているのを知りたい!」
興味を持つことで学習意欲が高まり、自分の未来に役立つ知識として受け止めるようになります。
保護者の皆さまへのご提案
ご家庭でも、次のような方法でお子さまの学びをサポートしてみてください。
- 身近な例を考える:
- 「スマホがどうやって現在地を知るのか」を一緒に調べてみる。
- 地図アプリを使って、現在地の特定や距離を測る体験をする。
- 一緒に疑問を探る:
- 「この道具はどう動いているの?」といった疑問を一緒に考え、答えを探す楽しさを共有する。
- 褒めて励ます:
- 「よく考えたね!」とお子さまの発想や努力を認め、自信を育む。
まとめ
中学数学で学ぶ平面図形の内容は、私たちの生活に密接に関係しています。カーナビやスマホといった身近な技術が、教科書の内容と結びついていることを知ることで、子どもたちは学ぶことの楽しさと重要性を実感します。
私たちは、これからもお子さま一人ひとりの学びを全力でサポートしていきます。何かご質問やご不安な点がございましたら、どうぞお気軽にご相談ください!

カーナビと平面図形-min.jpg)
