よく耳にする危険なセリフ 「習っていません。」
どの単元の話でもいいのですが、ちょうどこの時期 ６年生が「比」を習うので、「比」を題材にお話をします。
なぜか不思議に軽く触れる程度で終わってしまう単元です。 比も割合も、同じことを違った形で表現しているだけなのに、そのことも説明しないまま終わってしまいます。
そこに踏み込めば、パーセントも割合も単位量も、つまり、数学の文章問題の最重要ポイントも理科の計算問題もほとんどが片付いてしまいます。マックスでは、この方法を採用しています。
本当にこんなに楽で、便利な方法は、めったになのに、そこまで踏み込まないであっさりと終わってしまいます。
％や割合を苦手にする中学生に、理科の計算問題に苦しんでいる子たちに、算数内容を「比」を使って教え直しをすると、ほとんどの子が「えっ？ そんなに簡単なの？」と不思議な顔をします。いずれ、そんな時が、お子さんにも来ると思います。
今回はその話ではなくて、「比」を材料にした別の話をします。 これは基本中の基本の話です。
２ ： ３ ＝ ｘ ： ６ これを解くのに、小学校の段階では方程式は習っていませんから、内項の積 ＝ 外項の積 は使えません。
では、どうするかといえば、左辺の後項の３が、右辺では６になっている。２倍になっているから、左辺の前項の２も２倍されて、右辺では４になると考えます。
ここまでは、みんな大丈夫なんです。問題は、分数や小数が出てきたら… その時にどう反応するか。
たとえば、こんな問題です。 
どうですか？ 3 → 6 は、パッと２倍とわかりますね。
いよいよ今日のテーマです。
は、 パッと何倍か、わかりますか。
基礎力がある子なら、3 → 6 が瞬間的に２倍とわかるように も、一呼吸置くぐらいで、何倍かがわかります。
これは基礎力が出来上がっているかどうかのチェックポイントとして私がよく使う問題のひとつです。最近では一呼吸置いても答えが出ない子が主流派となっています。
大多数の人は、この段階で思考停止状態。「習っていない」と言い始めます。悲しい現実です。 習っていない訳でもないのですが、考えることもしません。いや、できないのかも。
基礎の基礎で、やさしく考えれば。
1はすべての基本です。しかし、基礎力がない子は、基本を使えません。
どういうことかといえば、 を考えていますが、ここで真ん中に、基本の数 1をはさみます。
そうすると、
となります。
前半は、
を1にするから
です。 [基礎事項確認： ◯を◯でわると1になる]
後半は、 1を1/3にするから、
です。[基礎事項確認： 1に◯をかけると◯になる]
これで、 は、 
だとわかります。
このように、流れを追って筋道を立てていく力が考える力なんです。勉強って、考えるって、この力＝筋道を立てていく力を身につけることです。
思い出しました。 以前、このような説明をしていたら、特別何も指示していないのに、赤ペンで、自分のノートに下記のように書いた子がいました。
○ ： △ ＝ □ ： ◇ → □ ＝ ○ ÷ △ × ◇
小６の女の子です。
いや。 正直、驚きました。上記ような説明から、これだけの一般化した「まとめノート」が作れるのは、すごい。たいしたものです。
中３生でも、かなり勉強に慣れてこないと（毎年、秋以降、初冬ぐらいにようやく）、「まとめノート」が作れるようになるかなぁって状態です。本当にすごいです。 拍手。
この子が、「おもしろい。こんな問題もっとないの」と興味を示した問題を挙げてみます。ちなみに、その問題を中学生にやらせてみました。反応は、予想通り。「習っていません」。
では、見てみましょう。
「月齢」って何？
「月齢」は小学校でも中学校でも習いません。
でも、でもですよ。問題文をよく読めば、「月齢」についての考え方は書いてあります。だから、問題を解く前に「月齢」に関する知識は、ゼロで大丈夫です。 知識の問題ではなくて思考の問題です。
「習っていない」とは、
「考えられません」という告白！
と言うことは、「習っていない」と言うことさえも、すでにピント外れの反応なのです。最大の問題は、「習っていない」と考えることを止めてしまう姿勢・考え方にあります。
「習っていない」って、実は「考えられません」という状態を表現している言葉だったのです。だから、子どもの「習っていない」発言に、「そうなの。習ってないんじゃしょうがないね」なんで思うことはやめにしましょう。
この手の問題が要求していることは、筋道を立てて進んでいけということなのです。必要な情報はすべて書いてあります。
ルールに従って筋道を立てて進めていく力が考える力です。ＩＴ時代の今日、多くの情報はカンタンに集めることができます。その情報から筋道を立てて、何を考えることができるのか？ それが、子どもたちが将来、働くようになったときに問われることです。その力を鍛えるために、今 勉強しているわけです。それを、「習ってない」と放棄しているって、将来「ヤバくねぇ」ってことです。
せっかくなので問題を説明しておきます。
まず、潮位の差は、図１よりAが約170cm。図２より Bが約100cmです。
表の中から潮位の差をもとに、Ａの日とＢの日を探すと、Aの日の候補 ：②、③、④ Bの日の候補 ：⑥、⑦、⑧です。
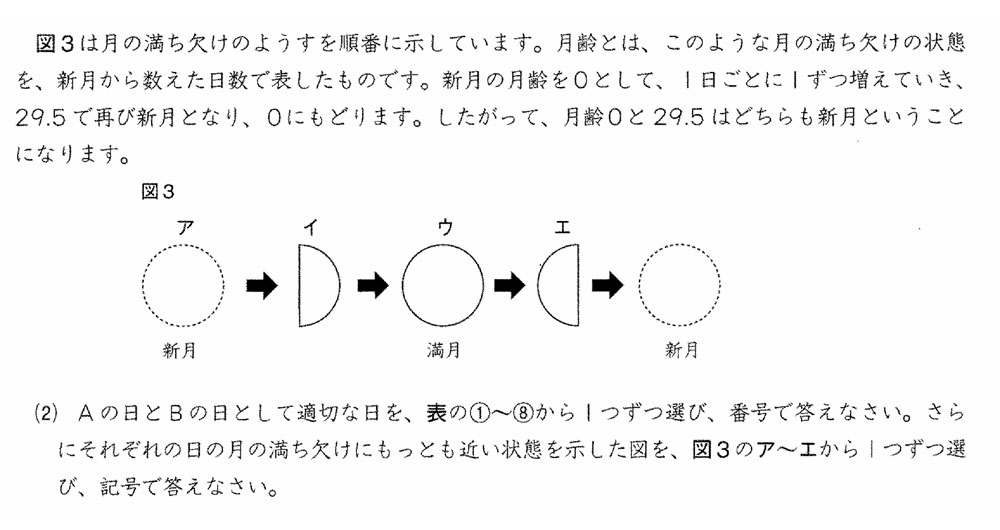
次に、月の満ち欠けと月齢の説明を読むと、月の満ち欠けは、新月から始まって、次の新月までが１サイクルで、このサイクルがグルグル回ります。
月齢は新月が、0と29.5と言うことなので、図３の左の新月の月齢が0、右の新月の月齢が29.5となります。小数を無視して、29.5は約30だから、ウの月の月齢はその半分で約15。イは、アとウの中間だから、イの月齢は約7、エの月齢は約22とわかります。これで、月の形と月齢がわかりました。
また、「Aの日とBの日は、７日違う」と問題文にありました。「月齢は１日ごとに １ずつ増える」と説明があったので、Aの日の月齢とBの日の月齢も７違うはずです。
と言うことは、 Aが②（月齢29.4）だとすると、Bは⑥（月齢イ6.9）です。 Aが③だとすると、Bは該当する日はありません。 Aが④（月齢14.9）だとすると、Bは⑧（月齢21.9）です。
解答
（1） より適している日はＡの日
（理由） Ａの日は午前１１時ごろに潮位がもっとも低いから。
（2） 答えは２通りあります。
１つ目：Ａの日 ④ 月の形 ウ、 Ｂの日 ⑧ 月の形 エ
２つ目：Ａの日 ② 月の形 ア 、Ｂの日 ⑥ 月の形 イ
◆鶴ヶ谷教室 ☎252-0998
989-0824 宮城野区鶴ヶ谷4-3-1
◆幸 町 教室 ☎295-3303
983-0836 宮城野区幸町3-4-19
電話でのお問合せ AM10:30～PM22:30