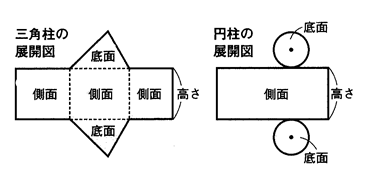
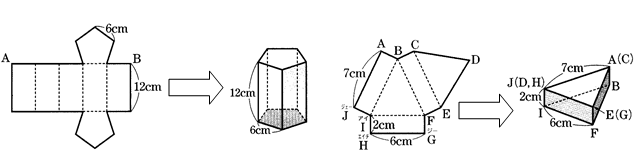
文章問題が得意な子の特徴とは?
教室で子どもたちを指導していると、伸びる子とそうでない子の違いが明確にわかります。例えば、伸びる子は鉛筆を持つ手が自然と動くのに対し、そうでない子は手が止まってしまうことが多いのです。
伸びる子は、説明を聞きながら「アッ」と思ったことをすぐにノートにメモします。自分で問題を解くときも、計算だけでなく、途中の式や考えたことをしっかり書き残します。一方、伸び悩む子のノートは答えだけがきれいに並んでいることが多く、考えた過程が見えません。
最大の違いは「わからない」と思ったときの行動!
文章問題を一読しただけでは答えが出せないとき、子どもたちの反応には大きな違いが見られます。
✅ 伸びる子 → 問題の意図を図や表にして整理し、計算を試みる
✅ 伸び悩む子 → 「わからない」「できない」「習っていない」と思考を止めてしまう。しかし、考えるための具体的なステップを示すことで、手を動かす習慣を身につけることができます。例えば、「まず問題文の大事な部分に線を引く」「登場する数や関係をリスト化する」「簡単な式を試しに立ててみる」など、小さなアクションを取り入れることが効果的です。
こうした違いが、文章問題への得意・不得意を分ける要因になっています。
では、どうすれば文章問題を得意になれるのでしょうか?
考える力をつけるには?
考えるときには「手を動かす」ことが重要!
今度の休みに何をしようか考えるときは、頭の中だけで想像することができます。でも、旅行の計画や家計簿を考えるときは、メモを取って整理しませんか?
脳科学の研究でも、「考えるときは手を動かせ」と言われています。
伸びる子は、問題を図や表に整理する習慣がついています。 もちろん、適当に書き殴るわけではなく、先生が使った図を自分で描きながら理解を深めていくのです。
自分で図を描けるようになろう!
文章問題を得意にするためには、図を描いて考える力をつけることが不可欠です。
✅ 伸びる子 → 先生の図をマネし、自分で描く練習をする
✅ 伸び悩む子 → 先生の図を見て「わかった気になる」だけで終わる
大切なのは、「自力で図を描けるようになること」です!
対応表を活用しよう!
割合・速さ・人口密度・1あたりの量など、文章問題の多くは対応表を使えばスムーズに考えられるようになります。
例えば、春集中授業以降も、時間にゆとりのある週2回コースでは、
📌 図の書き方・作り方・活用方法 をじっくり指導
📌 対応表を使うことで、自分の頭で考えられるようになる
例 : 「6個で300円の消しゴム1個の値段は何円ですか」
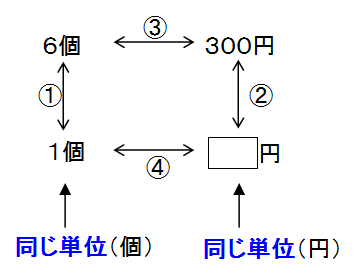
●同じ単位の数をたてに並べる
①,②は同じ関係。 ①は下から上に6倍(×6)だから、逆に上から下は÷6 ②も上から下は÷6になるから、 (答)300円÷6=50円 小6で、ここに分数が登場します。分数があってもまったく同じことをするだけです。
この指導を9月まで継続し、重要単元を確実にマスターしていきます。
線分図を描く習慣をつけよう!
例えば、次の問題を考えてみましょう。
(問題)
公園で1日に集めたアルミ缶とスチール缶の合計は152個でした。 スチール缶の数は、アルミ缶の数の3倍より16個多くありました。 それぞれ何個ずつあったでしょう?(小4後半レベル)
この問題は、線分図を描くことでスムーズに解くことができます。
(解き方)

- 線分図を描く
- アルミ缶の数の4倍+16個が合計152個とわかる
- 152-16=136(アルミ缶の4倍)
- 136÷4=34(アルミ缶の数)
- 34×3+16=118(スチール缶の数)
✅ 答え:アルミ缶34個、スチール缶118個
この問題で本当に学ぶべきことは、「線分図を自分で描けるようになること」です!
📌 人が描いた図を見て理解するだけでは、考える力はつかない! 📌 自分で図を描けるようになることが大事!
考える力は技術であり、練習で身につく!
考える力とは、問題の意図を図や表に整理する力です。
これはトレーニングすれば確実に身につく技術です!
✅ 手を動かすことを習慣にする!(例えば、毎日のミニ練習として「3分間で問題のキーワードに線を引く」「簡単な図を描いてみる」などを取り入れると、手を動かす習慣が自然と身につきます。また、ご家庭では、「今日の問題の図を見せて説明してみよう」と声をかけることで、学習を振り返る機会を作るのも効果的です。)
✅ 先生の図をマネして、自分で描く練習をする!
✅ 対応表・線分図を活用する!(例えば、速さの問題で「道のり=速さ×時間」の関係を整理する際に、対応表を使うとどの値を求めるのかが明確になります。また、割合の問題では、全体と部分の関係を線分図で表すことで、計算の手順がスムーズに理解できます。)
この技術を身につけた子どもたちは、どんどん伸びていきます。例えば、ある生徒は最初、文章問題に苦手意識を持っていましたが、毎日少しずつ線分図を描く練習を続けた結果、3ヶ月後には模試の得点が大幅に向上しました。また、計算ミスが多かった生徒も、対応表を活用することで情報を整理できるようになり、問題を解くスピードと正確性がアップしました。
なぜなら、「考える力」を持っているからです!
この春、考える力を鍛えて、文章問題が得意な子になりましょう!

◆鶴ヶ谷教室 ☎252-0998 989-0824 宮城野区鶴ヶ谷4-3-1
◆幸 町 教室 ☎295-3303 983-0836 宮城野区幸町3-4-19
電話でのお問合せ AM10:30~PM22:30