「うちの子、文章問題になると…」その悩み、合格屋マックスが解決します！
「計算は得意なのに、文章問題になると、途端に鉛筆が止まってしまう…」
そんな悩みをお持ちの保護者の方、実は少なくありません。
計算問題はスラスラ解けるのに、文章問題になると、解き方が分からず、自信をなくしてしまうお子様が意外と多いんです。
「計算はできるのに、応用問題になると解けない」というお子様をこれまで数多く見てきました。
そこで今回は、小学4年生で実際に行った授業内容を例に、「算数の本当の面白さ」とその指導法をお伝えします。
大切なのは「考える姿勢」
ある日、生徒にこんな問題を出題しました。
公園で1日に集めたアルミ缶とスチール缶は、合わせて152個でした。スチール缶の数は、アルミ缶の数の3倍より16個多くありました。それぞれ何個ずつあったでしょう。
この問題、解き方以前に、 子どもたちが問題に対してどんな行動をとるか を観察することが重要です。
例えば、問題文を前に眉間にしわを寄せながら、鉛筆を動かしたり止めたり、試行錯誤している様子が見られたら、それは素晴らしいことです！
問題文に線を引いたり、図を描こうとしたり、自分なりの方法で解決策を見つけようと格闘している証拠です。
10分以上ああでもない、こうでもないと試行錯誤する経験こそが、応用問題を解くための土台となるからです。合格屋マックスでは、 「考える姿勢」 を大切にしています。
「見える化」で、算数が得意になる！
では、実際にどのように問題に取り組めば良いのでしょうか？
合格屋マックスでは、「見える化」をキーワードに指導を行っています。
例えば、先ほどのアルミ缶とスチール缶の問題。
- まずは問題文を読み解き、アルミ缶とスチール缶の数の関係を図に表してみましょう。
- 図を描くことで、アルミ缶とスチール缶の合計が「アルミ缶の4倍＋16個」であることに気がつきます。
- あとは、図を頼りに、計算していくことで答えを導き出すことができます。
「見える化」 図を描けば、問題が見えますね。
（アルミかんの４倍）＋（１６こ）が１５２こです。
１５２－１６＝１３６ … アルミかんの４倍の数
１３６÷４＝３４ … アルミかんの数
３４×３＝１０２ … スチールかんの数 答え） アルミかん３４個 スチールかん１０２個
このように、図や絵を活用することで、複雑な問題も分かりやすく整理することができます。
図形問題
図形問題は、「考える姿勢」 を養うために絶好の問題です。
このような問題に対して、頭の中で立体をイメージできるようになることが重要です。
授業では、実際に積み木を使ったり、展開図を描いたりしながら、まずは楽しみながら空間把握力を高めていきます。
この形が、一体どんな立体になるのか。見える化できるかが最大のポイントですね。
まずは一番左側。 正面から見ると３つ。上から見ると４つだから、
こんな感じです。
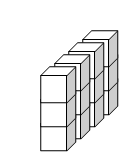
でも、最も少ない積み木でという条件があるから、正面から３つ、上から４つに見えるには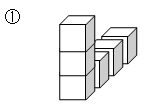
こんな具合に図を描いてみて、
（正面から見た図） と（上から見た図） をあわせて考えると、
（横） から見たときの形ががわかる。 な～んだ。簡単じゃん。
② 左から２番目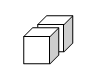 
③ 左から３番目 
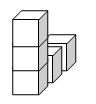④ 一番右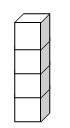 
①、②、③、④を全部たして、１７個でできている。
「算数＝計算」ではない！
「算数＝計算」から、「算数＝考える力、筋道を立てて考える力」に算数の重点が移って来ています。
だから、ただ単に、公式を丸暗記するのではなく、考える技術としての見える化する技術の習得が大きポイントになっています。
「考える楽しさ」「わかる喜び」を、お子様にも
合格屋マックスは、「算数＝考える力、筋道を立てて考える力」という考えのもと、子どもたちの「考える力」を育むことを目指しています。
- わからない問題にぶつかっても、諦めずに試行錯誤する力
- 問題を整理し、分かりやすく「見える化」する力
- 論理的に考え、答えを導き出す力
これらの力は、算数だけでなく、将来社会に出ても必ず役に立つはずです。
「うちの子も、算数の楽しさを知ってほしい！」
そう思われる方は、ぜひ合格屋マックスにご相談ください。
お友達と楽しく学ぶことで、相乗効果が生まれ、学習意欲の向上に繋がることもあります。
高校・中学で問われる内容は、算数とは少し違う。小学生～高校生までを教えているからこそわかる、考える力を伸ばすポイント・ずっと伸びていけるポイントが身につくように教えています。
小学5年生の壁！「倍数と約数」、合格屋マックス流で攻略！
今回は、小学5年生がつまずきやすい単元の一つ、「倍数と約数」についてお話します。
「あれ？うちの子、分数になると急に計算が遅くなった…？」
「文章問題で、最小公倍数という言葉が出てくると、手が止まってしまう…」
もしかしたら、それは「倍数と約数」がしっかり理解できていないことが原因かもしれません。
小学5年生になると、分数計算はもちろん、割合や比など、これまで以上に複雑な計算が増えていきます。
「倍数と約数」は、これらの計算の基礎となるため、この時期につまずいてしまうと、その後の算数学習に大きな影響が出てしまう可能性も…😥
そこで今回は、「倍数と約数」でつまずく原因と、合格屋マックスが実践する効果的な指導法について、具体的に解説していきます！
なぜ「倍数と約数」でつまずくの？
「倍数と約数」は、抽象的な概念を理解する必要があるため、それまで順調に算数を学習してきたお子様でも、つまずきやすいポイントです。
しかし、この単元をしっかり理解することは、その後の 分数計算（通分や約分）の基礎 となるため、非常に重要です。小学5・6年生で学習する割合や比の計算など、複雑な計算にも関わってきます。
合格屋マックス流！「倍数と約数」を分かりやすく！
合格屋マックスでは、「倍数と約数」を、より具体的に、そして「見える化」して学習することで、お子様たちが無理なく理解を深められるよう指導しています。
例えば…
問題：6と10の最小公倍数を求めよ。
最初は、実際に数字を書き出して考えてみましょう！
- 6の倍数：6, 12, 18, 24, 30…
- 10の倍数：10, 20, 30, 40…
このように書き出すことで、6と10の共通の倍数（公倍数）が30, 60…と見つけることができ、最小公倍数が30であることが分かります。
問題：たて12cm、横18cmの長方形があります。この中に同じ大きさの正方形を敷き詰めます。1辺が何cmの正方形を敷き詰めることができますか。すべて答えなさい。また、一番大きな正方形は何枚必要ですか。
この問題は、図を使うことで理解がぐっと深まります。
- まず、長方形の中に正方形を敷き詰める様子をイメージしてみましょう。
- 正方形の1辺の長さは、長方形のたてと横の両方を割り切れる数である必要があります。
- つまり、12と18の公約数を求めればよいことが分かります。
- 12と18の公約数は、1, 2, 3, 6 です。
- したがって、1辺が1cm、2cm、3cm、6cmの正方形を敷き詰めることができます。
一番大きな正方形は、1辺が6cmなので、たてに2つ(12 ÷ 6 = 2)、横に3つ(18 ÷ 6 = 3)並びます。
よって、一番大きな正方形は 6枚 必要です。
「倍数と約数」をマスターして、分数計算も楽々クリア！
「倍数と約数」は、その後の分数計算の基礎となるだけでなく、割合や比など、小学5・6年生で習う重要な単元の土台にもなります。
合格屋マックスでは、お子様一人ひとりの理解度に応じて、説明方法を柔軟に変更しながら、丁寧に指導しています。「うちの子は算数が苦手…」と不安を感じている保護者の方も、ぜひ一度、合格屋マックスにご相談ください。
